Theorie: Betrachtung einer aktiven Tone- Control Klangregelung

In meinem Beitrag „Vorbetrachtung: Planung eines Audio-DSP Mixers“ habe ich bereits eine Vorbetrachtung zur Entwicklung eines analogen Kanalzugs mit aktiver Klangreglung durchgeführt. Da es noch ein wenig dauert bis die Platinen und Bauteile für dieses Unterprojekt geliefert werden, möchte ich die Zeit nutzen um die Funktionsweise der aktiven Tone- Control Schaltung etwas nachvollziehbarer zu beschreiben.

Die folgende Betrachtung fokussiert sich auf phänomenologische Zusammenhänge, auf vollständige Berechnungen möchte ich zunächst verzichten.

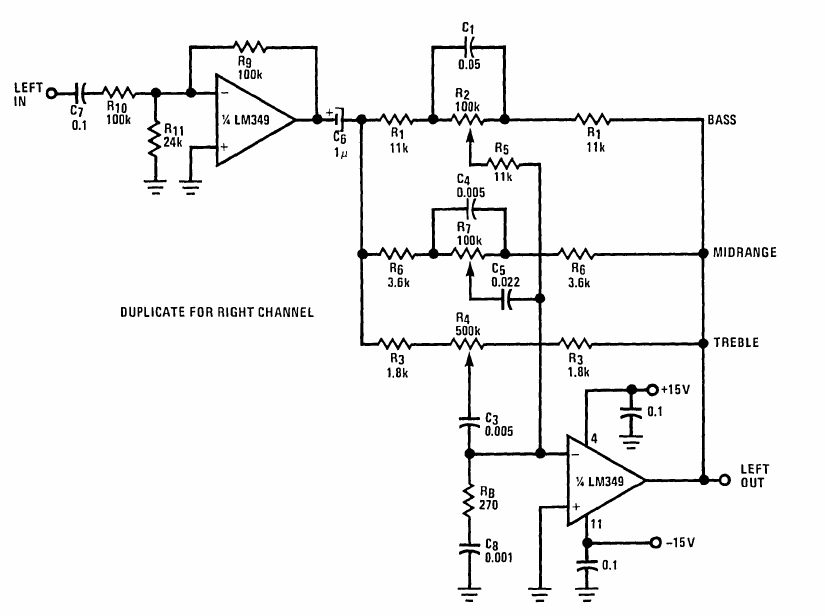
Pic 1 zeigt die Vorlage der Tone- Control Schaltung, wie ich sie im erwähnten Unterprojekt verwendet habe. Ignoriert man den Eingangsverstärker oben links im Bild, besteht die Schaltung aus einem invertierenden Operationsverstärker, welchem mehrere Rückkopplungspfade zugeführt werden. Im Folgenden werde ich von einem einfach rückgekoppelten Verstärker ausgehend die resultierende Verstärkung betrachten und dann nach und nach die passiven Bauelemente der Tone- Control Schaltung hinzufügen.

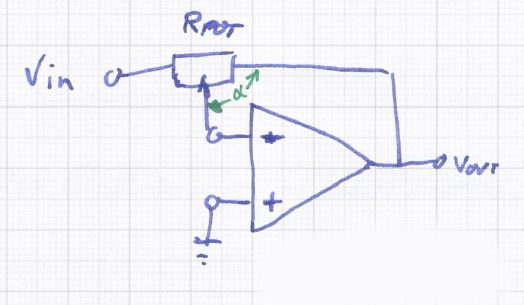
Pic 2 zeigt einen einfachen, als Invertierer beschalteten Operationsverstärker. Das Potentiometer R_{POT} ist in jedem Rückkopplungspfad in Pic 1 enthalten und stellt einen Spannungsteiler zwischen der Eingangsspannung v_{in} und der Ausgangsspannung v_{out} dar, dessen Abgriff dem invertierenden Eingang des Verstärkers zugeführt ist. Die Variable \alpha repräsentiert die Potentiometerstellung von R_{POT}. Diese legt fest, wie groß der Anteil von R_{POT} ist, der dem Ausgang des Verstärkers zugeneigt ist. Analog bestimmt sie die reduktion des v_{in} zugeneigten Anteil von R_{POT}. Mathematisch sei es wie folgt festgehalten:

Eqn 1: Anteil von R_{POT} zu v_{out}:

R_{R_{POT} \text{ zu } v_{out}} = \alpha R_{POT}

Eqn 2: Anteil von R_{POT} zu v_{in}:

R_{R_{POT}\text{ zu }v_{in}} = (1-\alpha)R_{POT}

Wobei gilt:

\alpha \in \mathbb{R} \{ 0 \leq \alpha \leq 1 \}

Angewandt auf die Gleichung zur Bestimmung der Ausgangsspannung des invertierenden Verstärkers (nach Michael Reisch ISBN: 978-3-540-34014-0 Springer Verlag), lässt sich die Ausgangsspannung des Verstärkers aus Pic 2 berechnen via Eqn 3:

v_{out} = - \frac{\alpha R_{POT}}{(1-\alpha)R_{POT}} v_{in} = - \frac{\alpha}{1 - \alpha} v_{in}

Teilt man beide Seiten durch v_{in} erhält man die Übertragungsfunktion H(j\omega) Eqn 4:

H(j\omega) = - \frac{\alpha}{1 - \alpha}

Der Betrag der Übertragungsfunktion ist bislang unabhängig von der Signalfrequenz und eine Grenzwertbetrachtung liefert die Auswirkung der Vollausschläge des Potentiometers (\alpha \to 0, bzw. \alpha \to 1) Eqn 5:

\lim_{\alpha \to 0} H(j\omega) = - \frac{0}{1 - 0} = 0 \\
\text{} \\
\lim_{\alpha \to 1} H(j\omega) = - \frac{1}{1 - 1} = "\infty"

Weil die Rückkopplungspfade in Pic 1 jeweils mit einem Frequenzband korrespondieren, lässt diese Betrachtung darauf schließen, dass die Potentiometer (In Pic 1 als R_2, R_7 und R_4 bezeichnet) für die Anhebung, bzw. Absenkung der jeweiligen Frequenzbereiche verantwortlich sind. Rein rechnerisch bedeutet dies eine Anhebung von -\infty Dezibel, bzw. \infty Dezibel, wobei eine unendliche positive Anhebung den Operationsverstärker natürlich in die Sättigung treibt.

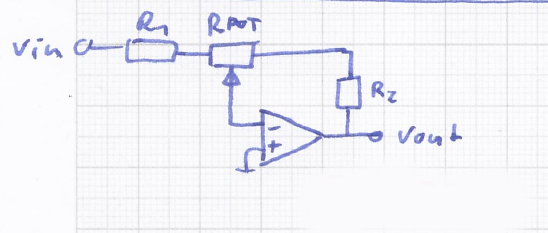
Pic 3 zeigt die Ergänzung der Schaltung um die Widerstände R_1 und R_2. Das Prinzip der Schaltung ist exakt das gleiche wie bisher, jedoch muss hier nun Der Anteil von R_{POT} zu v_{in} um R_1 vergrößert werden, sowie der Anteil von R_{POT} zu v_{out} um R_2 vergrößert werden muss. Die neue Übertragungsfunktion H_1(j\omega) ist demnach Eqn 6:

H_1(j\omega) = - \frac{\alpha R_{R_{POT}}+ R_2}{(1-\alpha) R_{R_{POT}}+ R_1}

Eine erneute Grenzwertbetrachtung liefert Eqn 7:

\lim_{\alpha \to 0} H_1(j\omega) = - \frac{R_2}{R_{R_{POT}} + R_1} \\
\text{} \\
\lim_{\alpha \to 1} H_1(j\omega) = - \frac{R_{R_{POT}}+R_2}{R_1}

Der Grenzwert für \alpha \to 0 zeigt, dass durch die Anwesenheit von R_2 \gt 0 die Verstärkung nicht auf null reduziert werden kann. Analog zeigt der Grenzwert für \alpha \to 1, dass der Nenner des Terms durch die Anwesenheit von R_1 \gt 0 nicht null wird, woraus eine endliche Verstärkung resultiert.

Aus dieser Betrachtung lässt sich festhalten, dass die Widerstände in Pic 1 (dort bezeichnet als R_1, R_6 und R_3) die Verstärkung des jeweiligen Frequenzbereichs eingrenzen. Die minimale und maximale Verstärkung kann durch das Gleichsetzen der Beträge der Grenzwerte aus Eqn 7 mit den gewünschten Verstärkungen eingestellt werden, wobei auch der Wert des Potentiometers R_{R_{POT}} eine Rolle spielt.

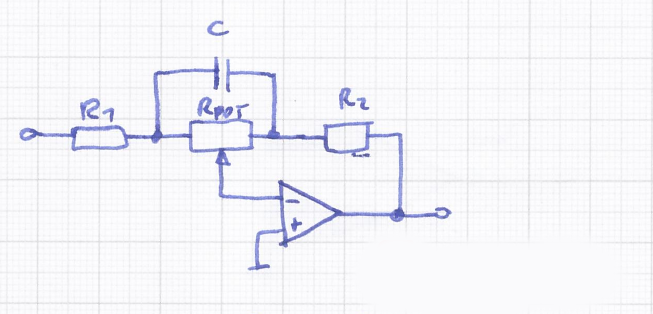
In Pic 4 wird die Schaltung nun mit einer Kapazität C parallel zum Potentiometer erweitert. Um die Übertragunsfunktion dieser Schaltung zu bestimmen ist es nötig eine Dreieck- Sternumwandlung durchzuführen. Da die Dreiecksglieder aus unterschiedlichen passiven Elementen bestehen, gilt eine so ermittelte Übertragungsfunktion lediglich für eine bestimmte Frequenz. Da sich die Schaltung aber bei Extremwerten von der Frequenz f und von \alpha vereinfachen lässt (AC-DC Analyse), werden zunächst diese Fälle untersucht.

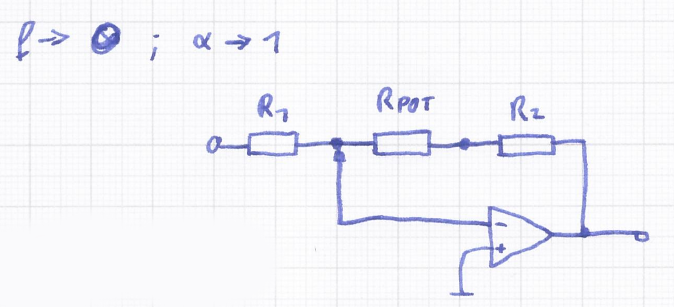
H_2(j\omega)_{f = 0, \alpha = 1} = - \frac{R_{R_{POT}}+R_2}{R_1} \\
\text{mit } \omega = 2\pi f

Eqn 8: Übertragungsfunktion für f = 0 und \alpha = 1

Ist die Signalfrequenz f gleich null, steigt die Impedanz X_C der Kapazität über alle Grenzen, weshalb die Kapazität C praktisch keinen Einfluss auf die Schaltung hat. Die Übertragungsfunktion für \alpha gleich 1 (Eqn 8) gleicht daher der Bekannten Übertragungsfunktion aus Eqn 7.

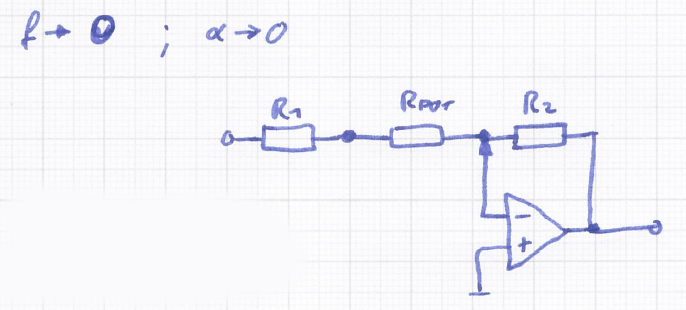
H_3(j\omega)_{f = 0, \alpha = 0} = - \frac{R_2}{R_1 + R_{R_{POT}}}\\
\text{mit } \omega = 2\pi f

Eqn 9: Übertragungsfunktion für f = 0 und \alpha = 0

Das Selbe gilt für die Übertragungsfunktion für \alpha gleich null (Eqn 9).

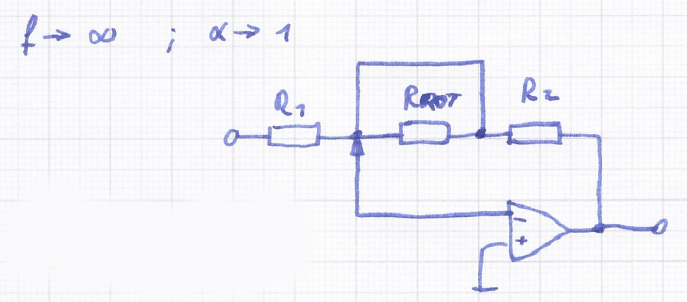
H_4(j\omega)_{f = "\infty", \alpha=1} = -\frac{R_2}{R_1}\\
\text{mit } \omega = 2\pi f

Eqn 10: Übertragungsfunktion für f = "\infty" und \alpha = 1

Der andere Extremfall gilt für Signale mit unendlich hoher Frequenz. Da die Impedanz der Kapazität praktisch zu null wird, stellt diese einen Kurzschluss parallel zum Potentiometer dar.

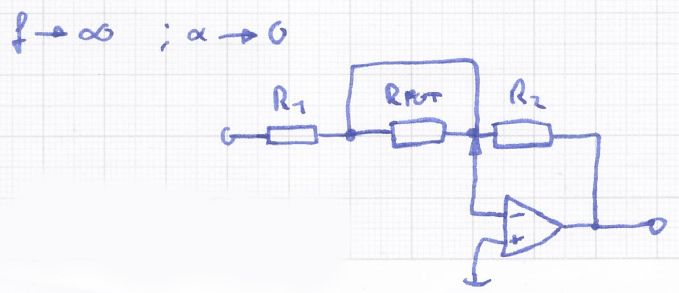
H_5(j\omega)_{f="\infty",\alpha=0} = - \frac{R_2}{R_1}\\
\text{mit } \omega = 2\pi f

Eqn 11: Übertragungsfunktion für f = "\infty" und \alpha = 0

In den Extremstellungen des Potentiometers führt dieser quasi- Kurzschluss dazu, dass das Potentiometer praktisch überbrückt wird, weshalb der Widerstand des Potentiometers keine Rolle für die Übertragungsfunkion spielt. Eqn 10 und Eqn 11 sind daher identisch und proportional zu \frac{R_2}{R_1}.

Betrachtet man weiterhin die Schaltung mit dem Potentiometer in seinen Extremstellungen (sprich \alpha = 1 und \alpha = 0), so kann man das Potentiometer R_{POT} und die Kapazität C als parallel geschaltet (X_C || R_{POT}) auffassen. Eqn 12:

X_C || R_{R_{POT}} = \left( j2 \pi f_C C + (R_{R_{POT}})^{-1} \right)^{-1} \\
\text{} \\
= \left( \frac{j2 \pi f_C C R_{R_{POT}}+1}{R_{R_{POT}}} \right)^{-1} \\
\text{} \\
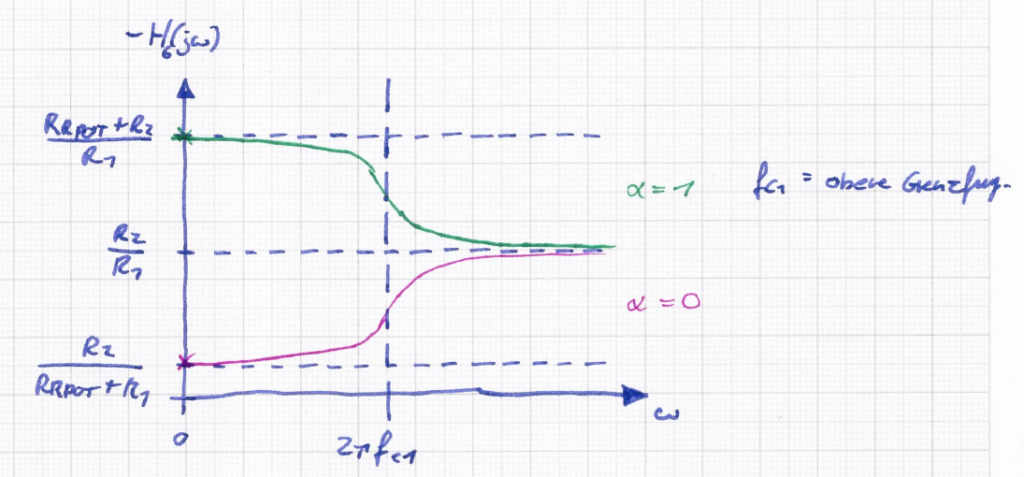
= \frac{R_{R_{POT}}}{j2 \pi f_C C R_{R_{POT}}+1}

Dadurch ist es bereits möglich, einen Amplitudengang für minimale und maximale Potentiometerstellung vorherzusagen. Eqn 13:

H_6(j\omega)_{\alpha = 1} = - \frac{(X_C || R_{R_{POT}})+R_2}{R_1} = - \frac{\frac{R_{R_{POT}}}{2\pi f_c C R_{R_{POT}}+1}+R_2}{R_1}\\
\text{} \\
H_6(j\omega)_{\alpha = 0} = - \frac{R_2}{(X_C || R_{R_{POT}}) + R_1} = - \frac{R_2}{\frac{R_{R_{POT}}}{2\pi f_c C R_{R_{POT}}+1} + R_1}

Weiter zeigt Eqn 13, dass die Lage des Passbandbereiches mit der aktuellen Beschaltung lediglich von C und R_{R_{POT}} anhängt.

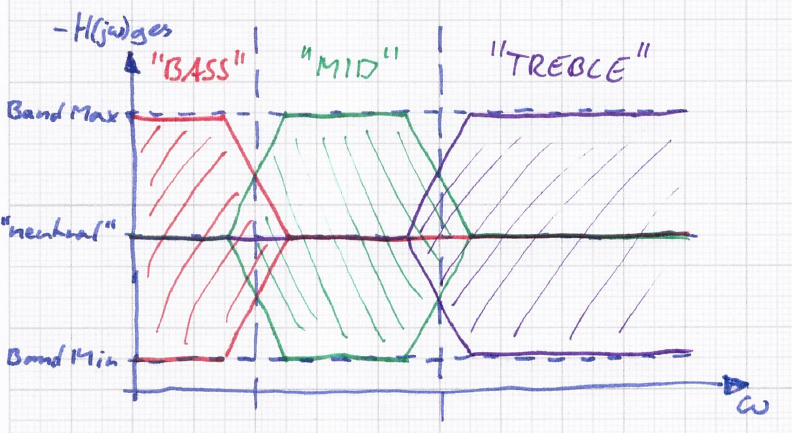
Under Construction…

Der Beitrag wird fortgesetzt…